Agenda 1ra clase:
- Teoría semántica operacional
- Metodología de la práctica
- Actividad con nota
Semántica operacional
Temas:
- Árboles
- Árbol sintáctico abstracto
- Sistema de transición
- Big step vs small step
- Notación secuente
Bibliografía:
- Plotkin. A Structural Approach to Operational Semantics. (descarga aquí legalmente)
- Pierce. Types and programming languages.
Árboles en ocaml
type tree = Node of tree * tree
| Leave of string
let a1:tree = Leave "hola"
let a2:tree = Node(
Leave "izq",
Leave "der"
)
let a3:tree = Node(
Node(
Leave "izq",
Leave "der"
),
Leave "masder"
)
Árboles en ocaml
type tree = Node of tree * tree
| Leave of string
let a1:tree = Leave "hola"
let a2:tree = Node(
Leave "izq",
Leave "der"
)
let a3:tree = Node(
Node(
Leave "izq",
Leave "der"
),
Leave "masder"
)
Árboles en ocaml
type tree = Node of tree * tree
| Leave of string
let a1:tree = Leave "hola"
let a2:tree = Node(
Leave "izq",
Leave "der"
)
let a3:tree = Node(
Node(
Leave "izq",
Leave "der"
),
Leave "masder"
)
Árboles en ocaml
type tree = Node of tree * tree
| Leave of string
let a1:tree = Leave "hola"
let a2:tree = Node(
Leave "izq",
Leave "der"
)
let a3:tree = Node(
Node(
Leave "izq",
Leave "der"
),
Leave "masder"
)
AST: Árbol de sintaxis abstracto
float matchO(char *s) { /* find a zero */
if (!strncmp(s, "0.0", 3))
return 0.;
}
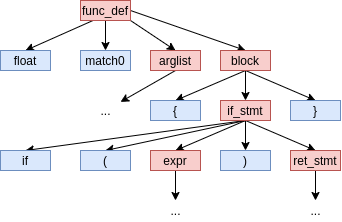
AST: Árbol de sintaxis abstracto
type expr = Lit of int | Sum of expr * expr | Times of expr * expr
2 * 3 + 1
Sum(
Times(Lit 2, Lit 3),
Lit 1
)
1 * 2 * 3
Times(
Lit 1
Times(Lit 2, Lit 3),
)
(1 * 2) * 3
Times(
Times(Lit 1, Lit 2),
Lit 3
)
Ejercicio interactivo
https://replit.com/@jisbruzzi/ex1-structural-recursion-ocaml
Sistemas de transición[Plotkin 1.2]
- Dupla $(\Gamma,\to)$
- $\Gamma$ conjunto de configuraciones
- $\to$ relación entre elementos de $\Gamma$.
- $\to \subset \Gamma \times \Gamma$
ST terminales[Plotkin 1.2]
- Tripla $(\Gamma,\to,T)$
- No se puede transicionar desde un elemento de $T\subset\Gamma$
- $\forall \gamma \in T \forall \gamma' \in \Gamma. \gamma \not\to \gamma'$
ST determinísticos [TAPL 3.5.4]
- $\to$ es una función
- $ \gamma\to\gamma' \land \gamma\to\gamma'' \implies \gamma'=\gamma''$
Ejemplo: lenguaje Switch
type operatons = Switch operations | End
type state = On|Off
type sconfig = operations*state

let c1=(Switch (Switch (Switch End)),On);;
let c2=(Switch (Switch End),Off);;
let c3=(Switch End,On);;
let c4=(End,Off);;
(Switch(x),On)$\to$(x,Off)(Switch(x),Off)$\to$(x,On)- $T=\{$
(End,On),(End,Off)$\}$
(Switch(x),On)$\to$(x,Off)(Switch(x),Off)$\to$(x,On)- $T=\{$
(End,On),(End,Off)$\}$
type operatons = Switch operations | End
type state = On|Off
type sconfig = operations*state
exception Terminal
let small_step (config:sconfig):sconfig =
match config with
| (Switch x, On) -> (x, Off)
| (Switch x, Off) -> (x, On)
| (End, _) -> raise Terminal;;
let rec big_step (config:sconfig):sconfig =
match config with
| (Switch End, On) -> (End,Off)
| (Switch End, Off) -> (End, On)
| (Switch x, On) -> big_step (x,Off)
| (Switch x, Off) -> big_step (x, On)
| (End, _) -> raise Terminal;;
Ejemplo: lenguage pp
Aclaración: listas
type operation = Push of int | Times | Add
type ppconfig = (operation list * int list)
(Push x::tl,s)$\to$(tl,x::s)(Add::tl,a::b::s)$\to$(tl,(a+b)::s)(Times::tl,a::b::s)$\to$(tl,(a*b)::s)- $T=\{$
([],x)$\}$
let e1 = ( Push 3::Push 2::Push 4::Add::Times::Times::[] , [8]);;
let e2 = ( Push 2::Push 4::Add::Times::Times::[] , [3;8]);;
let e3 = ( Push 4::Add::Times::Times::[] , [2;3;8]);;
let e4 = ( Add::Times::Times::[] , [4;2;3;8]);;
let e5 = ( Times::Times::[] , [6;3;8]);;
let e6 = ( Times::[] , [18;8]);;
let e6 = ( [] , [144]);;(* e6 pertenece a T *)
let x = ( Add::[] , [99]);;(* ? *)
let y = ( [] , [37;15;2]);;(* ? *)
Big step vs small step
-
Lenguage PP:
([Push 1; Push 2;Add];[])$\xrightarrow[]{PPs}$([Push 2;Add];[1])([Push 1; Push 2;Add];[])$\xrightarrow[]{PPb}$([];[3]) -
Lenguage Switch:
(Switch (Switch (Switch End)),On)$\xrightarrow[]{Ss}$((Switch (Switch End),Off)(Switch (Switch (Switch End)),On)$\xrightarrow[]{Sb}$(End,Off) -
Lenguage lits:
3*4+2*3$\xrightarrow[]{Ls}$12+2*33*4+2*3$\xrightarrow[]{Lb}$18
3*4+2*3
12+2*3
12+6
18
$T=\{$ Lit(_) $\}$
type expr = Lit of int | Sum of expr * expr | Times of expr * expr
type litconfig = expr
exception Terminal
exception Implementar
let big_step (c:litconfig):litconfig = match c with
| Lit(_) -> raise Terminal
| x -> Lit(eval x);;
let small_step (c:litconfig):litconfig = match c with
| Lit(_) -> raise Terminal
| Sum(Lit x, Lit y) -> Lit (x + y)
| _ -> raise Implementar;;
Ejercicio interactivo
https://replit.com/@jisbruzzi/ex2-small-step-lits
Notación secuente (sequent calculus)
Se escribe:
$$ \begin{array}{c c c} A & B & C \end{array} \over D $$
$$
{\htmlClass{orange}{x} \to \htmlClass{green}{x'}}\over{Sum(\htmlClass{orange}{x},y)\to
Sum(\htmlClass{green}{x'},y)}
$$
$$
{\htmlClass{orange}{y} \to \htmlClass{green}{y'}}\over{Sum(Lit(x),\htmlClass{orange}{y})\to
Sum(Lit(x),\htmlClass{green}{y'})}
$$
$$
{}\over{Sum(Lit(\htmlClass{orange}{x}),Lit(\htmlClass{green}{y}))\to
Lit(\htmlClass{orange}{x}+\htmlClass{green}{y})}
$$
Sistema de transición de lits
type litconfig = Lit of int
| Sum of litconfig * litconfig
| Times of litconfig * litconfig
$$
{\htmlClass{orange}{x} \to \htmlClass{green}{x'}}\over{Sum(\htmlClass{orange}{x},y)\to
Sum(\htmlClass{green}{x'},y)}
$$
$$
{\htmlClass{orange}{y} \to \htmlClass{green}{y'}}\over{Sum(Lit(x),\htmlClass{orange}{y})\to
Sum(Lit(x),\htmlClass{green}{y'})}
$$
$$
{}\over{Sum(Lit(\htmlClass{orange}{x}),Lit(\htmlClass{green}{y}))\to
Lit(\htmlClass{orange}{x}+\htmlClass{green}{y})}
$$
$$
{\htmlClass{orange}{x} \to \htmlClass{green}{x'}}\over{Times(\htmlClass{orange}{x},y)\to
Times(\htmlClass{green}{x'},y)}
$$
$$
{\htmlClass{orange}{y} \to
\htmlClass{green}{y'}}\over{Times(Lit(x),\htmlClass{orange}{y})\to
Times(Lit(x),\htmlClass{green}{y'})}
$$
$$
{}\over{Times(Lit(\htmlClass{orange}{x}),Lit(\htmlClass{green}{y}))\to
Lit(\htmlClass{orange}{x}*\htmlClass{green}{y})}
$$
$T=\{$
Lit(_) $\}$¿Preguntas?
A continuación, laboratorio.