Analizadores Sintácticos
Analizador Sintáctico SLR Canónico#
En un tabla LR(0) cada celda solo puede contener a lo sumo una producción o celdas vacías. Esto asegura que dicha tabla puede realizar análisis sintáctico de gramáticas LR(0).
Las tablas de análisis sintáctico LR(0) pueden tener conflictos:
Reduce / Reduce
Shift / Reduce
Conflicto Reduce/Reduce#
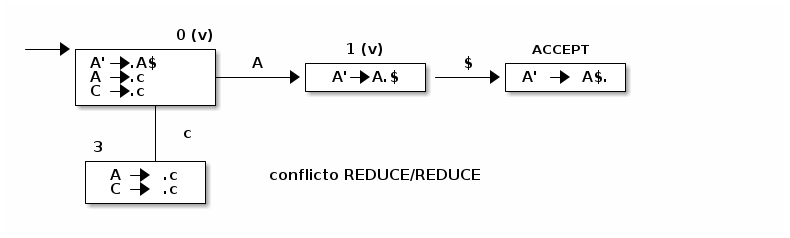
Se producen cuando hay dos elementos A→ α. en el mismo estado.
Dada la gramática G=({A', A, C}, {c | $}, P A') con el siguiente conjunto de producciones:
A' → A$
A → c | C
C → c
Se construye un autómata de las siguientes características
| estado | A' | A | C | c |
|---|---|---|---|---|
| …. | ||||
| 3 | A→c / C→c | |||
Conflicto Shift/Reduce#
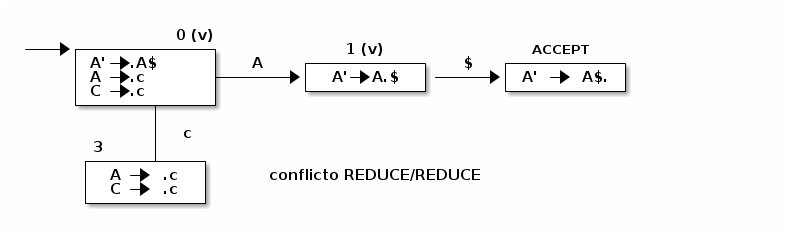
Este tipo de conflicto se da cuando un elemento de la forma A→ α. y un elemento que no tiene esa forma se encuentran en una misma celda de un estado.
G=({E',E,A}, {a,b$}, P ,E' ) cuyo conjunto de producciones es
E' → E$
E → A | Ab
A → a | ab
En este caso hay ambigüedad en la gramática, al generar el autómata se obtiene:
El análisis sintáctico LR(0) puede presentar conflictos. Para ello se mejora el algoritmo utilizando el llamado SLR
#Análisis Sintáctico Ascendente SLR#
- es una variante del LR(0), incrementa de manera importante la potencia del análisis al utilizar el token SIGUIENTE en la cadena de entrada para dirigir sus acciones.
- Las Acciones REDUCE no ocupan todas la fila de la tabla.
- Solamente se reduce por una producción A→β para los símbolos terminales que puedan aparecer a continuación de A.
- Se pone ACTION[q,a]=REDUCE(A→β) solamente cuando a pertenece a SIGUIENTE(A).
- La idea es cuando se completa la tabla se pone ACTION[q,a]=Reduce(A→β) solo si a ∈ SIGUIENTE(A)
- Esto evita conflictos:
- Reduce / Reduce
- Shift /Reduce
Ejemplo#
Sea G=({S',A, S},{a,b,$},P,S' ). Con el conjunto P:
S' → S$
S → a | Ab
A → a
Se genera el autómata LR(0):
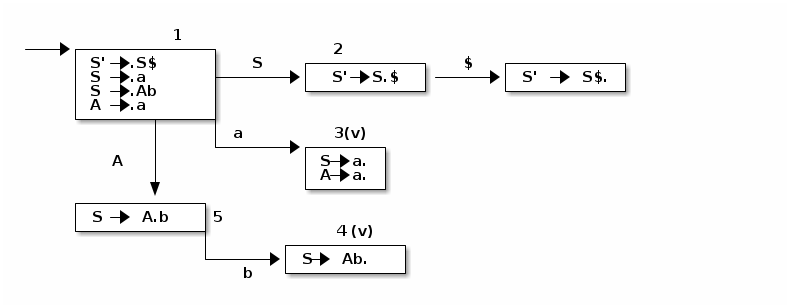
Tabla LR
( recordar que cada vez que se tiene un elemento con un punto al final se ponene las acciones reduce en todos los no terminales.
| estado | S' | S | A | a | b | $ | |
|---|---|---|---|---|---|---|---|
| 1 | 2 | 5 | S3 | ||||
| 2 | Accept | ||||||
| 3 | S→a / A→a | S->a / A→a | S→a / A→a | S→a / A→a | |||
| 4 | S→Ab | S→Ab | S→Ab | ||||
| 5 | s4 |
No hay tabla LR(0) ya que hay un conflicto Reduce / Reduce en el estado 3
La idea es que las producciones no vayan en todas las filas, sino que las el elemento A → a. van en las columnas que contengan a SIGUIENTE(A)
No terminales PRIMERO SIGUIENTE S {a} {$} A {a} {b} S' {a} {$} Se construye la tabla SLR teniendo en cuenta lo anterior
| estado | S' | S | A | a | b | $ |
|---|---|---|---|---|---|---|
| 1 | 2 | 5 | S3 | |||
| 2 | ||||||
| 3 | A→a | S→a | ||||
| 4 | S→ab | |||||
| 5 | s4 |
- Las gramáticas SLR no son ambiguas, pero hat gramáticas no ambiguas que no son SLR
G=({S,L,R}, {id,=,*}), P, S)
S → L=R | R
L → * R | id
R → L
Analizador sintáctico LR(1) Canónico#
Usa un token lookahead
El concepto detrás es el de refinar aun más el autómata: si el siguiente símbolo de la entrada es a, solo se debe reducir por A → β cuando a podría venir a continuación de A
Está construido de tal forma que mantiene el registro de cual es el símbolo de debería venir a continuación tal que si A → β. /a donde /a es el lookahead
Elemento LR(1)#
Un elemento LR(1) es un par [A →α.β donde A → αβ es una producción y a ∈ |SigmaU {$} es un símbolo terminal.
- Los estados de la tabla de Análisis Sintáctico LR(1) son Ahora conjuntos de elementos LR(1)
- La tabla se construye igual que la LR(0), la parte más importante es la definición de elemento LR(1) y su Clausura.
Clausura De un Elemento LR(1)
Entrada: una gramática un conjunto de elementos LR(1)
Salida: CLAUSURA(E)
J=E while hay cambios for each elemento [A-> alpha . beta,a] pertenece a J for each producción B-> gamma for each simbolo terminal b que pertenece a PRIMERO(betaa) J=J U {[B-.gamma,b]} end end end end- Ejemplo :
Sea G=({S',S,A}, {a,b,$},P, S'). Donde P es
S' → S
S → AA
A → aA | b
Construir el autómata:
Primeros
| no terminal | Primero |
|---|---|
| A | {a,b] |
| S | {a,b} |
Se hace la clausura
Analizador Sintáctico LR con lectura Anticipada LALR#
El tamaño de la tabla LR(1) es muy grande, a pesar de que el método es muy poderoso.
Se define núcleo de un conjunto de elementos como al subconjunto de elementos que no son de la forma [A→ .β/a]
Una vez construido el autómata LR(1) se identifican los estados que tienen el mismo núcleo sin tener en cuenta el lookahead y se fusionan en un solo estado para reducirla cantidad de estados del autómata.