Laboratorio 1: Resumen teórico

Breve repaso de DFA (Autómata Finito Determinístico)

Composición de un DFA

• Alfabeto $\Sigma$
• Conjunto de estados $D$
• Función de transición $T:D\times\Sigma\rightarrow D$
• Estado inicial $S_0 \in D$
• Estados de aceptación $A \subset D$

Un DFA es una tupla $(\Sigma,D,T,S_0,A)$.

Esta definición tiene su equivalente en código en el archivo common.ts, donde Alphabet ($\Sigma$) y State ($D$) son parámetros de tipo.

export interface MachineDescription<Alphabet, State> {  transition: Transition<Alphabet, State>;  initial: State;  acceptance: State[];}

Cómo visualizar un DFA

El siguiente DFA detecta un número impar de letras a.

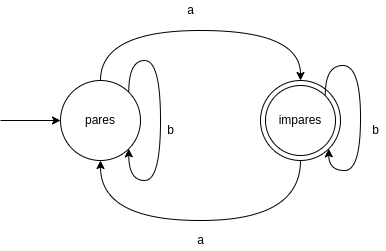
• Alfabeto $\Sigma$: letras sobre las transiciones
• Conjunto de estados $D$: cada círculo es un estado
• Función de transición $T:D\times\Sigma\rightarrow D$: flechas entre estados con una letra al lado
• Estado inicial $S_0 \in D$: La apunta una flecha que viene desde afuera
• Estados de aceptación $A \subset D$: Estado con un reborde.

Cómo describir un DFA

A continuación se describe el mismo DFA sin un diagrama.

• Alfabeto $\Sigma = \{a,b\}$
• Conjunto de estados $D=\{pares, impares\}$
• Estado inicial $S_0 = pares$
• Estados de aceptación $A={impares}$
• Función de transición $T:D\times\Sigma\rightarrow D$: tabla a continuación

estado	letra	nuevo estado
$pares$	$a$	$impares$
$pares$	$b$	$pares$
$impares$	$a$	$pares$
$impares$	$b$	$impares$

Para qué sirven las DFA

• Análisis estático que extrae DFA de tu código java
• Las expresiones regulares representan DFA
• redux usa conceptos similares
• Es una excelente forma de modelar el estado y los cambios de estado de nuestros programas